Euler Examples

Suche auf Euler Seiten

Optimierung - Beispiele

Wir rechnen einige Beispiele für Optimierung mit dem Simplex-Algorithmus und mit der Hand (unterstützt durch Euler) durch.

Das erste Beispiel besteht aus Kapazitätsbeschränkungen für eine Landwirt, der zwei Feldfrüchte anbauen möchte. Er hat 1000ha Fläche und 4500 Arbeitsstunden zur Verfügung. Das ergibt für ihn die Beschränkungen

Maximieren will er den Gewinn

Dazu geben wir alles in Matrixform ein.

>A=[1,1;4,5]

            1             1 
            4             5 

>b=[1000,4500]'

         1000 
         4500 

>c=[5,6]

[5,  6]

Euler kann bei zwei Variablen die Menge der zuläsigen Punkte als Polygon berechnen. Die Nebenbedingung hat dabei die Form

>x=feasibleArea(A,b);
>plot2d(x[1],x[2],filled=true,style="/");

Wir starten nun den Simplexalgorithmus, der ohne weitere Angaben das Problem

löst. Wir setzen das Flag für Maximierung. Das Flag für check erspart uns, den Ergebniscode zu überprüfen.

>v=simplex(A,b,c,>max,>check)

          500 
          500 

Nun plotten wir den optimalen Punkt und die Niveaulinie der Zielfunktion.

>function map f(x,y) := c.[x;y]
>plot2d("f",level=c.v,>add);
>plot2d(v[1],v[2],points=true,style="ow",>add):

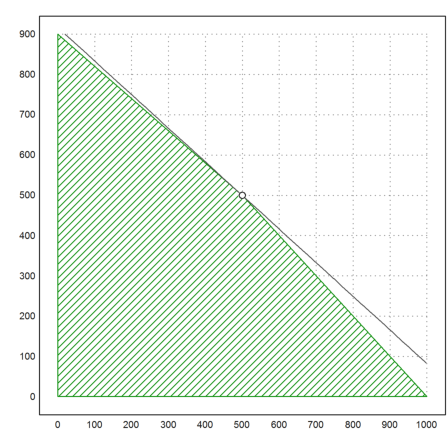
Der Wert der Zielfunktion ist 5500.

>c.v

5500

Das duale Problem lautet

Man kann das so deuten, dass der Landwirt sein gesamtes Land und seine gesamte Arbeitskraft zu Preisen p1 bzw. p2 möglichst günstig anbietet, so dass es auf jeden Fall für ihn günstiger wird, als wenn er alles selbst vermarkten würde.

Wir lösen es, wobei wir durch den vierten Parameter eq=1 die Ungleichungen als >= kennzeichnen.

>p=simplex(A',c',b',eq=1,>min,>check)

            1 
            1 

>b'.p

5500

Ändert man die Zielfunktion ein wenig ab, so ergibt sich ein Minimum, das die Ressourcen nicht voll ausschöpft.

>c=[5,7];
>x=feasibleArea(A,b); ...
 plot2d(x[1],x[2],filled=true,style="/"); ...
 v=simplex(A,b,c,>max,>check), ...
 plot2d("f",level=c.v,>add); ...
 plot2d(v[1],v[2],points=true,style="ow",>add):

            0 
          900 

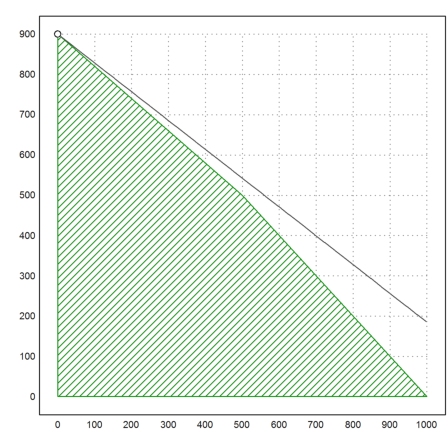
Im dualen Problem erkennt man, dass der Landwirt den Preis so festsetzt, dass die erste Feldfrucht nicht abgerufen wird, da er daran mehr verdienen würde als durch eigene Disposition.

>p=simplex(A',c',b',eq=1,>min,>check); A'.p-c'

          0.6 
            0 

Ein Transportproblem

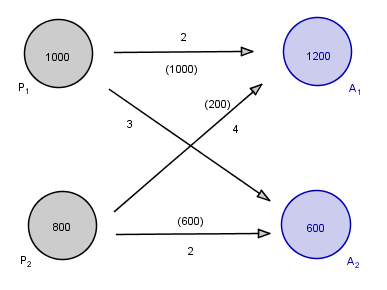
Wir lösen das Transportproblem, bei dem aus zwei Lagern zwei Produktionsstätten beliefert werden sollen. Die Menge, die dabei von Lager i nach Ort j geschickt werden, nennen wir c(i,j). Die Kosten seien

Die zur Verfüngung stehenden Mengen und die benötigten Mengen ergeben Restriktionen

>shortformat;

Die Spalten der Matrix entsprechen den Variablen

>A=[1,1,0,0;0,0,1,1;1,0,1,0;0,1,0,1]

        1         1         0         0 
        0         0         1         1 
        1         0         1         0 
        0         1         0         1 

>b=[1000,800,1200,600]'

     1000 
      800 
     1200 
      600 

Die Ungleichungen sind zweimal <= und einmal >=.

>eq=[-1,-1,1,1]'

       -1 
       -1 
        1 
        1 

>c=[2,3,4,2]

[2,  3,  4,  2]

Es ergibt sich die Lösung, die auch in Klammern im obigen Bild angedeutet ist.

>x=simplex(A,b,c,eq=eq,>min,>check)

     1000 
        0 
      200 
      600 

Das duale Problem hat auch hier eine Deutung.

Statt die Lieferung selbst zu machen, verkaufen wir die Ware in den Lagern zu Preisen p1, p2 und kaufen sie wieder zu Preisen q1, q2 ein, wo sie gebraucht wird. Die Differenz der Verkaufspreise darf nicht größer als die Transportkosten sein, also etwa

Die Preise gestalten wir so, dass der Vertragsnehmer möglichst viel Gewinn macht.

Der Einfachheit halber schreiben wir alles in Form von <=. Das geht durch Multiplikation von A und b mit -eq.

>p=simplex(-(eq*A)',c',-(eq*b)',>max,>check)

        2 
        4 
        0 
        2 

Wir erhalten dasselbe Optimum.

>-(eq*b)'.p, c.x

4000
4000

Examples Homepage